Die Mondlandefähre war zu instabil, um zu fliegen. Sie hätte unmöglich auf einer schmalen Schubsäule balancieren können. Jede Bewegung der Astronauten hätte sie unkontrollierbar ins Taumeln gebracht.

Dieses spezielle Stabilitätsproblem ist so alt wie die Raketentechnik selbst. Das Beharren der Verschwörungstheoretiker darauf, dass dies speziell für die Mondlandefähre ein Problem darstellt, zeigt ihren Mangel an Wissen und Erfahrung im Bereich der Raketenwissenschaft. Tatsächlich muss jede Rakete auf ihrer "Schubsäule" "balancieren", egal, ob sie nun aufwärts oder abwärts fliegt. Oder wissenschaftlicher ausgedrückt: der Schubvektor muss jederzeit ziemlich genau durch das Massezentrum der Rakete zeigen, um ungewünschte Rotation zu vermeiden.

Windböen können jede Rakete plötzlich in die falsche Richtung ablenken. Und die Abnahme des Treibstoffvorrats verursacht eine ständige Veränderung des Schwerpunkts. Daher muss jede erfolgreiche Rakete ihren Schubvektor anpassen, wenn sich der Schwerpunkt verändert und auch sonst in der Lage sein, Rotationen, die durch innere und äußere Einflüsse verursacht werden, entgegenzuwirken.

Im Lauf der Jahrhunderte haben die Rakentenwissenschaftler verschiedene geniale Methoden angewandt, um dies zu erreichen.

Abb. 1 -Die klassische Rakete benutzt einen hölzernen Stab, als Heck. Da die Rakete rotiert, zwingt der Luftwiderstand am Heck sie zurück auf eine gerade Bahn.

Die klassische frühe Luftrakete in Abb. 1 verbindet die eigentliche Rakete mit einem langen Stab. Der Stab wird durch die Luft hinterhergezogen und hilft damit, die Rakete auf einem geraden Kurs zu halten, ähnlich wie die Heckflossen späterer Raketen. Indem er eine große aerodynamische Fläche hinter dem Schwerpunkt der Rakete anbrachte, und unter Berücksichtigung der Tatsache, dass alle Rotationen um den Masseschwerpunkt herum geschehen, konnte der Raketenbauer so erreichen, dass der Luftwiderstand das Heck der Rakete wieder in die Lotrechte hinter dem Masseschwerpunkt zurückdrückt.

Abb. 2 -Robert Goddards Rakete von 1926. Die Brennkammer (A) befand sich oberhalb des Treibstofftanks (B).

Dr. Robert Goddards frühe Raketen benutzen ein anderes Prinzip. Abb. 2 zeigt seine Rakete mit Flüssigantrieb von 1926. Treibstoff ist der schwerste Teil jeder Rakete, also plazierte Goddard ihn unterhalb der Brennkammer und der Austrittsdüse. Der Düsenschlund ist der Schubansatzpunkt, also nahm Goddard an, dass der Schwerpunkt (schätzungsweise irgendwo knapp oberhalb des Treibstofftanks), wenn er darunter hägt, sich selbst wie ein Pendel unter dem Schub der Rakete stabilisieren würde.

Es stellte sich heraus, dass dies nicht der Fall war: es macht keinen Unterschied, ob der Schubansatzpunkt sich oberhalb oder unterhalb des Schwerpunkts befindet. Und da es unpraktisch ist, den Treibstoffvorrat unterhalb der Düse anzubringen, wo er von den heißen Abgasen getroffen wird, kehrte Goddard zum traditionellen Aufbau mit dem Treibstoff oben zurück und brachte breite Heckflossen an, um aerodynamische Stabilisierung zu erreichen.

Das ist passive Stabilisierung -- die Rakete wird so konstruiert, dass jedes Kippen aus der Bahn automatisch in einer Kraft resultiert, die sie zurück in die Bahn bringt. Aktive Formen der Stabilisation wurden ebenfalls in Betracht gezogen, speziell für Rotationskräfte, die die Korrekturmöglichkeiten der passiven Stabilisation überstiegen. Das ist extrem wichtig für militärische und andere Raketen, die ihr Ziel sehr präzise anfliegen müssen.

Die frühen Raketenwissenschaftler erkannten, dass sie, wenn sie vorhersehen konnten, dass die Rakete kippen würde und schnell genug eine Korrektur anbringen könnten, sie das Kippen abfangen könnten, bevor es zu einem verhängnisvollen Taumeln wird. Um das Kippen festzustellen braucht man einen Bezugspunkt, an dem man die Orientierung der Rakete messen kann. Dann braucht man eine Möglichkeit, die Rakete zurück auf ihre vorgesehene Bahn zu rotieren. Und all das muß schnell genug geschehen, um die Rotation abzufangen, bevor sie zu schwerwiegend wird.

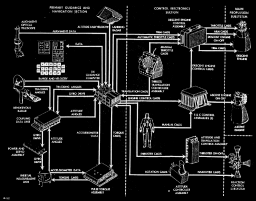
Hier ist eine detailliertere Darstellung, wie dies üblicherweise bewerkstelligt wird.

ALL DIES ZUSAMMEN IN DER MONDLANDEFÄHRE

Die aktiven Formen der Stabilisierung waren sehr wichtig beim Entwurf der Mondlandefähre, da hier keine Luft auf Leitwerke einwirken und die Rakete neu ausrichten kann, wenn ihre Achse in eine andere Richtung als ihre Flugbahn zeigt. Aerodynamische Stabilisierung schied aus. Deshalb erdachten die Konstrukteure der Mondlandefähre ein ausgeklügeltes computergesteuertes aktives Leitsystem.

Die Mondlandefähre bestand aus zwei Stufen, eine für den Abstieg und die andere für die Rückkehr in den Mondorbit und das Rendezvous mit dem Kommandomodul. Der Antrieb der Abstiegsstufe konnte gedrosselt werden. Er war außerdem kardanisch aufgehängt und konnte bis zu 6° seitlich in jede Richtung geschwenkt werden. Und natürlich gab es ein Set von RCS Düsen.

Abb. 5 - Schematische Darstellung des primären Steuerungs- und Stabilisierungssystems der Mondlandefähre. Ein komplett eigenständiges System kann einspringen, wenn dieses versagt. Leserliche Version (141 KB). (Northrop Grumman)

Sehr wichtig ist auch, dass die Mondlandefähre nicht nur ein sondern zwei separate computerbasierende Steuerungssysteme besaß. Eines davon basierte auf der gleichen Hardware wie der Steuerungscomputer des Kommandomoduls. Das andere war viel einfacher aufgebaut und konnte nur dazu verwendet werden, die Landung abzubrechen und/oder in den Orbit zurückzukehren. Der Hauptsteuerungscomputer (Abb. 5) war dafür verantwortlich, die Ausrichtung der Mondlandefähre mehrmals in der Sekunde zu überprüfen und den Kardan des Antriebs auszurichten, um sie in der Balance zu halten. Die Behauptung der Verschwörungstheoretiker, dass es das Fahrzeug aus dem Gleichgewicht gebracht hätte, wenn einer der Astronauten im Cockpit sein Gewicht verlagert hätte, entbehrt jeder Grundlage. Tatsächlich sah es so aus, dass wenn einer der Astronauten einen Schritt zur Seite gemacht und damit den Schwerpunkt der Landefähre verändert hätte, der Computer die notwendigen Anpassungen bereits ausgeführt hätte, bevor der Astronaut mit dem Schritt fertig war.

Eigentlich war die Mondlandefäre im Wesentlichen "fly-by-wire". Die Handsteuerung des Piloten hatte üblicherweise keine direkte Verbindung zum Antriebskardan oder dem RCS, obwohl es diese Möglichkeit gab. Meistens wurde einfach dem Computer übermittelt, in welche Richtung sich die Landefähre bewegen sollte -- links, rechts, vorwärts oder rückwärts. Der Computer veränderte dann den Kardanwinkel für die gewünschte laterale Bewegung. Der Pilot mußte nicht manuell die Balance der Landefähre aufrechterhalten.

Das Problem veränderlicher Masseschwerpunkte in Raketen war bereits in den 40er Jahren gelöst worden. Es ist einfach nur lächerlich anzunehmen, dass die Mondlandefähre in dieser Hinsicht irendwelche besonderen Schwierigkeiten verursachte. Tatsächlich sehen wir weiter unten, dass es in Wirklichkeit einfacher ist, das Taumeln der Landefähre zu verhindern, als eine normale zylindrische Rakete zu kontrollieren.

Aber der Antrieb der Aufstiegsstufe konnte nicht geschwenkt werden. Er war starr. Daher war sie zu instabil um zu fliegen.

Erstens: der selbe Computer, der den Abstieg kontrollierte, kontrollierte auch den Aufstieg. Das selbe RCS, das an der Kontrolle des Abstiegs beteiligt war, übernahm die gesamte Lagekontrolle für den Aufstieg. Wenn der Schub relativ zur Achse die Aufstiegsstufe zum Rotieren brachte, feuerten die RCS-Düsen, um der Rotation entgegenzuwirken und sie wieder die richtige Lage zu bringen. Daher zeigen Filme des Aufstiegs anscheinend ein periodisches Schwanken oder Schwingen: das RCS "kämpfte" gegen den Achswinkel des Aufstiegsantriebs an.

Fig. 6 - Frontansicht der Aufstiegsstufe der Mondlandefähre die die Treibstoff- und Oxidationsmittel-Tanks, das Austiegstriebwerk (grau), die Astronauten und die RCS-Düsen zeigt.

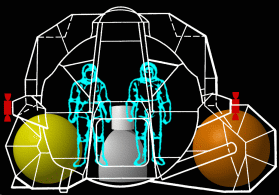
Zweitens: die Aufstiegsstufe der Mondlandefähre ist von Natur aus wesentlich stabiler als eine zylindrische Rakete, was die Trägheit angeht. (Man beachte, dass eine Rakete, die durch die Luft fliegt, diese Luft nutzen kann, sich zu stabilisieren.) Abb. 6 zeigt eine Frontalansicht der Aufstiegsstufe und die Position der Personen und Gegenstände, die den Schwerpunkt des Fahrzeugs beeinflussen.

Der Aufstiegsantrieb ist innerhalb, nicht unterhalb des Fahrzeugs angebracht. Dadurch befindet sich der Schwerpunkt sehr nah am Schubansatzpunkt, was die Rotationskräfte des von der Achse abweichenden Schubs mindert. Während der ersten Sekunden des Aufstiegs liegen der Schwerpunkt und der Schubansatzpunkt sehr eng beieinander.

Der massivste Bestandteil eines Raumfahrzeugs wie der Mondlandefähre ist der Treibstoff. Die Treibstofftanks werden so niedrig wie möglich montiert und sorgfältig an der Querachse ausbalanciert. (Das Oxidationsmittel ist dichter als der Treibstoff, daher liegt der Treibstofftank weiter außen). Obwohl in Abb. 6 nicht zu sehen, sind die Treibstofftanks für das RCS hinter den Astronauten montiert, was bei der Balance der Längsachse hilft.

Die Astronauten befinden sich zwischen den Treibstofftanks und sind beträchtlich weniger massiv. Außerdem wird ihre Bewegungsfreiheit durch die enge Kabine stark eingeschränkt. Insofern ignoriert die Idee, dass die Bewegungen der Astronauten einen stabilen Aufstieg verhindern würden, komplett die Tatsache, dass der wesentlich massivere Treibstoff weiter außen liegt und durch seine stetige Abnahme einen viel größeren Effekt bewirkt. Tatsächlich würden die massiven Treibstofftanks die Auswirkungen der Bewegungen der Astronauten dämpfen oder vermindern, so wie die lange Stange eines Seiltänzers seine Balance verbessert.

Man beachte außerdem die extrem weit außen liegende Position der RCS-Düsen. Sie sind an Auslegern montiert, um ihren Hebelarm zu verstärken (Rotationskraft). Für kleine Rotationen werden die Düsen im "Pulsmodus" gezündet, der sehr kurze Stöße benutzt.

ANATOMIE DES TAUMELNS

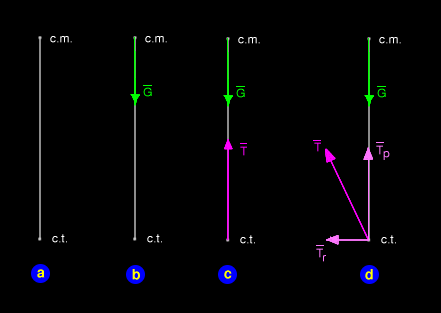
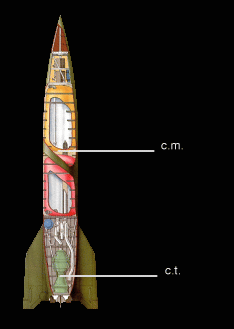
Die Theorie, wie man eine Rakete auf ihrem Schub ausbalanciert (unter Vernachlässigung aerodynamischer Effekte), ist ziemlich einfach. Bei den meisten Raumfahrzeugen sind der Schubansatzpunkt (c.t.) und der Masseschwerpunkt (c.m.) so angeordnet wie in Abb. 7a. Der Masseschwerpunkt ist der Punkt, um den das Raumfahrzeug naturgemäß rotieren wird und der, an dem die Gravitation (so vorhanden) wirkt (Abb. 7b). Der Schubansatzpunkt ist der Punkt, an dem die Kraft des Antriebs wirkt (Abb. 7c), im Allgemeinen der Düsenschlund.

Abb. 7 - Vektordiagram für von der Achse abweichenden Schub. (a) Die Beziehung zwischen dem Masseschwerpunkt "c.m." und dem Schubansatzpunkt "c.t." bei einer typischen Rakete. (b) Die Gravitation wirkt abwärts am Masseschwerpunkt. (c) Ein gut getrimmter Antrieb richtet seinen Schubvektor gegen den Masseschwerpunkt. (d) Wenn der Schub von der Achse abweicht, wirkt ein Teil des Schubes als Drehmoment am Schubansatzpunkt.

Wenn der Raketenantrieb korrekt getrimmt ist, wird er so geschwenkt, dass der Schubvektor (T in Abb. 7c) in einer Linie mit dem Schubansatzpunkt und dem Masseschwerpunkt liegt. Wenn sich allerdings der Masseschwerpunkt verändert -- z.B. wenn ein Astronaut sich bewegt oder der Treibstoff in den Tanks schwappt -- weist der Schubvektor nicht mehr in die richtige Richtung.

Abb. 8 - Die Auswirkung des Abstands vom Masseschwerpunkt (c.m.) auf das Drehmoment. (a) Bei größerem Abstand ist das Drehmoment stärker als bei einem geringeren Abstand (b).

Wenn dies geschieht, kann man sich T (in geometrischer Hinsicht "zerlegt") als eine Kombination eines Vektors T_p, der weiterhin in die richtige Richtung weist und weiter Schub liefert und T_r, der senkrecht zur Achse wirkt, vorstellen (Abb. 7d). Unser Interesse gilt hier T_r, weil durch ihn ein Drehmoment oder eine Rotationskraft auf das Raumfahrzeug wirkt. Ohne Korrektur wirkt diese Kraft weiter, und wird die Geschwindigkeit, mit der das Raumfahrzeug rotiert, erhöhen. In Abb. 7d lässt die Kraft das Raumfahrzeug im Uhrzeigersinn rotieren. Wenn die c.m./c.t.-Linie zu einer Horizontalen wird, wird der Antrieb überhaupt nicht mehr der Gravitation entgegenwirken. Die Komponente von T, die als Antrieb entlang dieser Achse wirkt -- T_p -- besitzt dann selbst keine Aufwärtskomponente mehr (T_p bezeichnet die lineare Komponente, T_r die Rotationskomponente).

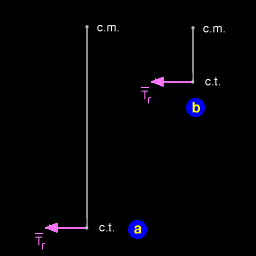
Betrachten wir für einen Moment nur die Rotationskomponente T_r. Wenn der Schubansatzpunkt weit entfernt vom Masseschwerpunkt liegt, wirkt T_r mit größerer Hebelkraft (Abb. 8a). Bewegt man den Antrieb näher an den Masseschwerpunkt (Abb. 8b), reduziert man die Hebelkraft und damit das Drehmoment oder die Drehkraft, die auf das Raumfahrzeug wirkt. Der Trick, ein Rohr auf den Griff eines Schraubenschlüssels zu schieben, um damit eine rostige Verbindung zu lösen, ist eine Anwendung dieses Prinzips.

Abb. 9 - Schnittzeichnugn der V2-Rakete. Der Masseschwerpunkt (c.m.) liegt vermutlich nahe am Mittelpunkt der Treibstofftankanordnung, nach hinten verschoben durch die Masse des Antriebs. (Abbildung mit Genehmigung von V2Rocket.com)

Die traditionelle Rakete (Abb. 9) besitzt einen weit oben liegenden Schwerpunkt. Der Schubansatzpunkt befindet sich immer am Heck. Das bedeutet, dass sich die traditionelle Rakete wie in Abb. 8a verhält, bei der das Drehmoment verstärkt wird. Folglich ist von der Achse abweichender Schub bei traditionellen Raketen ein viel größeres Problem als bei der Mondlandefähre (Abb. 6). Dort befindet sich der Schubansatzpunkt etwa auf Kniehöhe der Astronauten. Der sichtbare Masseschwerpunkt (unsere Schätzung des Masseschwerpunkts basierend auf dem geometrischen Zentrum des Querschnitts) liegt auf Brusthöhe der Astronauten. Somit ist die c.m./c.t.-Linie nur etwa einen Meter lang. Im Verhältnis zur Masse des Fahrzeugs wird von der Achse abweichender Schub bei der Mondlandefähre ein wesentlich geringeres Drehmoment haben als bei der V2.

Den größten Anteil an der Masse in der Aufstiegsstufe haben allerdings die Treibstofftanks, deren Mittelpunkte weit unterhalb des sichtbaren Schwerpunkts liegen. Dementsprechend verschiebt sich der Masseschwerpunkt nach unten. Obwohl die Berechnung des tatsächlichen Schwerpunkts ein sehr komplizierter und mühsamer Vorgang ist, können wir sicher sein, dass sich der Masseschwerpunkt nicht höher als in Brusthöhe der Astronauten, sondern wahrscheinlich viel niedriger -- möglicherweise sogar unterhalb des Schubansatzpunktes befindet.

Wie kann man behaupten, die Aufstiegsstufe der Mondlandefähre sei von Natur aus eine wesentlich stabilere Konstruktion? Das Trägheitsmoment einer zylindrischen Rakete ist viel größer als das der grob sphärischen Aufstiegsstufe. Das bedeutet, dass ein zylindrisches Raumfahrzeug dem Drehmoment viel stärker widersteht als ein sphärisches und damit eine bessere Konstruktion darstellt.

Gemäß der Physik ist diese Beobachtung zutreffend, allerdings wird dieser Effekt durch die Position des Antriebs in der Mondlandefähre und die daraus resultierende beachtliche Abschwächung des Moments überlagert.

EINEN MOMENT BITTE

Das "Trägheitsmoment" ist das Rotationsäquivalent der Masse. Newtons Gesetze der Mechanik sagen eindeutig aus, dass eine Masse Versuchen, sie in Bewegung zu versetzen (oder sie anzuhalten, wenn sie sich bereits in Bewegung befindet) Widerstand entgegensetzen wird, und dass dieser Widerstand proportional zur Masse des Objekts ist. Ebenso wird eine Masse Versuchen, sie in Rotation zu versetzen, Widerstand entgegensetzen, und dieser Widerstand ist proportional zu einer Kombination aus Masse und Form des Objekts. Lange, dünne Objekte widerstehen Änderungen der Rotation stärker als sphärische Objekte der gleichen Masse. Für jemanden, der schon einmal Bauholz getragen hat, ist das intuitiv einleuchtend. Wenn mal ein Brett schultert, balanciert man dessen Masseschwerpunkt auf der Schulter. Wenn man sich aber dabei herumdreht, wird man feststellen, dass das Brett die Drehbewegung nicht mitmachen und wenn es sich dann bewegt, nicht mehr anhalten will. Die Stabjonglage der Tambourmajore basiert auf dem hohen Trägheitsmoment solcher Objekte.

Stellen wir uns zwei hypothetische Raumschiffe von identischer Masse und identischem Volumen vor. Eines davon ist sphärisch, das andere zylindrisch. Die Länge des Zylinders beträgt das fünffache seines Durchmessers (willkürlich gewählter Wert). Der Radius des resultierenden Zylinders beträgt etwa die Hälfte des Radius des sphärischen Raumfahrzeugs.

In diesem Fall hat der Zylinder mehr als das fünffache Trägheitsmoment der Sphäre. Anders ausgedrückt würde man fünfmal soviel Drehmoment anwenden müssen, um die gleiche Rotationsrate wie bei der Sphäre auch beim Zylinder zu erreichen, obwohl ihre Masse gleich ist.

Aber wie wir oben gesehen haben, liegt die Antwort darin, wie nah am Schwerpunkt unser Antrieb untergebracht ist. Bei einem zylindrischen Raumfahrzeug (z.B. einer Rakete) sitzt der Antrieb an einem Ende des Zylinders. Wenn wir den Antrieb der Sphäre irgendwo an der Oberfläche unterbringen, wird der Antrieb des Zylinders etwa 2,5 mal soviel Drehmoment produzieren, weil er so weit vom Schwerpunkt entfernt ist. Wenn man das Trägheitsmoment mit einberechnet, wird die Rotationsbeschleunigung der Sphäre bei gleichem achsabweichendem Schub etwa zweimal so stark wie die des Zylinders sein.

Wenn, wie es bei der Aufstiegsstufe der Mondlandefähre der Fall ist, der Antrieb innerhalb der Sphäre und damit näher am Schwerpunkt liegt, wird das vom achsabweichenden Schub produzierte Drehmoment stark abgeschwächt. Tatsächlich müsste man ihn nur um die Hälfte des Radius nach innen verlegen, um die Situation auszugleichen, und wenn man ihn bei 1/3 des Radius anbringt, hat man eine stabilere Konstruktion als die des Zylinders erreicht, obwohl die Sphäre Rotation nicht so gut widersteht wie der Zylinder.

Der beste Nachweis für die Stabilität der Mondlandefähre ist empirisch. Nehmen Sie ein langes Lineal.Versuchen Sie, es senkrecht auf der Hand zu balancieren. Wahrscheinlich wird das nicht sehr lange gelingen. Balancieren Sie es jetzt waagerecht und benutzen sie die Einteilungen als Hilfsmittel um den Schwerpunkt zu bestimmen. Das sollte Ihnen sehr leicht fallen, und sie sollten sogar in der Lage sein, ihre Hand hin und her zu bewegen, ohne dass das Lineal dabei kippt. Masse und Moment sind in beiden Fällen gleich, aber Sie wenden weniger Drehmoment gegen die Achse an, wenn das Lineal waagerecht liegt.